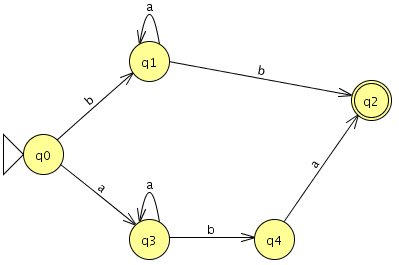
Aufgabe 1
Skizze
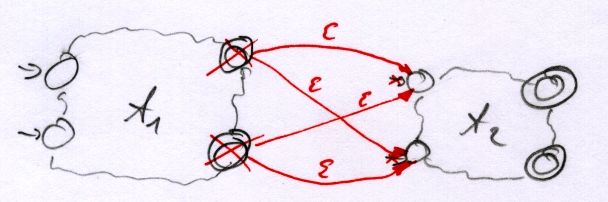
Gesuchtes
Gesucht ist `A = {Q,Sigma,delta,I,F} = A_1 @ A_2` (siehe dazu: Automatendefinition im Glossar). Anders ausgedrückt bedeutet das: "Welcher Automat ergibt sich aus der Konkatenation von `A_1` und `A_2`?".
Lösungsweg
Die Menge der Zustände von `A_1` wird mit den Mengen der Zuständen von `A_2` vereinigt.
`Q = Q_1 uu Q_2`.
Da das Eingabealphabet für beide Automaten identisch ist, bleibt es erhalten.
`Sigma = Sigma`
Alle Zustandsübergänge der beiden Automaten bleiben erhalten, werden also vereinigt. Dazu kommen die [`epsilon`-Übergänge glossar.html#epsilon-übergang], welche die Endzustände von `A_1` mit den Anfangszuständen von `A_2` verbinden.
`delta = delta_1 uu delta_2 uu F_1 x {epsilon} x I_2`
Die Anfangszustände des resultierenden Automaten kommen von `A_1`.
`I = I_1`
Die Endzustände kommen von `A_2`.
`F = F_2`
Antwort
Die vollständige Automatendefinition lautet `A={Q_1 uu Q_2, Sigma, delta_1 uu delta_2 uu F_1 x {epsilon} x I_2, I_1, F_2}`.
Aufgabe 2a
Potenzmengenkonstrukt
Erläuterungen dazu im Glossar.
| `delta_1` | `0` | `1` |
| `p` | `p,q` | `p` |
| `q` | `r` | `r` |
| `r` | `s` | - |
| `s` | `s` | `s` |
| `{p,q}` | `{p,q,r}` | `{p,r}` |
| `{p,q,r}` | `{p,q,r,s}` | `{p,r}` |
| `{p,r}` | `{p,q,s}` | `p` |
| `{p,q,s}` | `{p,q,r,s}` | `{p,r,s}` |
| `{p,q,r,s}` | `{p,q,r,s}` | `{p,r,s}` |
| `{p,r,s}` | `{p,q,r,s}` | `{p,r,s}` |
Die selbe Tabelle in Handschrift liegt hier und zeigt etwas besser, wie die Potenzmenge entsteht.
Transitionsdiagramm
Ausgehend von `p` wird der Automat aufgebaut. Alle Zustände, die `{s}` enthalten werden zu Endzuständen, denn im ursprünglichen Automaten ist `{s}` der Endzustand. Siehe auch Transitionsdiagramm im Glossar.

Aufgabe 2b
Potenzmengenkonstrukt
| `delta_2` | `0` | `1` |
| `p` | `q,s` | `q` |
| `q` | `r` | `q,r` |
| `r` | `s` | `p` |
| `s` | `-` | `p` |
| `{q,s}` | `{r}` | `{p,q,r}` |
| `{q,r}` | `{r,s}` | `{p,q,r}` |
| `{p,q,r}` | `{q,r,s}` | `{p,q,r}` |
| `{r,s}` | `{s}` | `{p}` |
| `{q,r,s}` | `{r,s}` | `{p,q,r}` |
Transitionsdiagramm
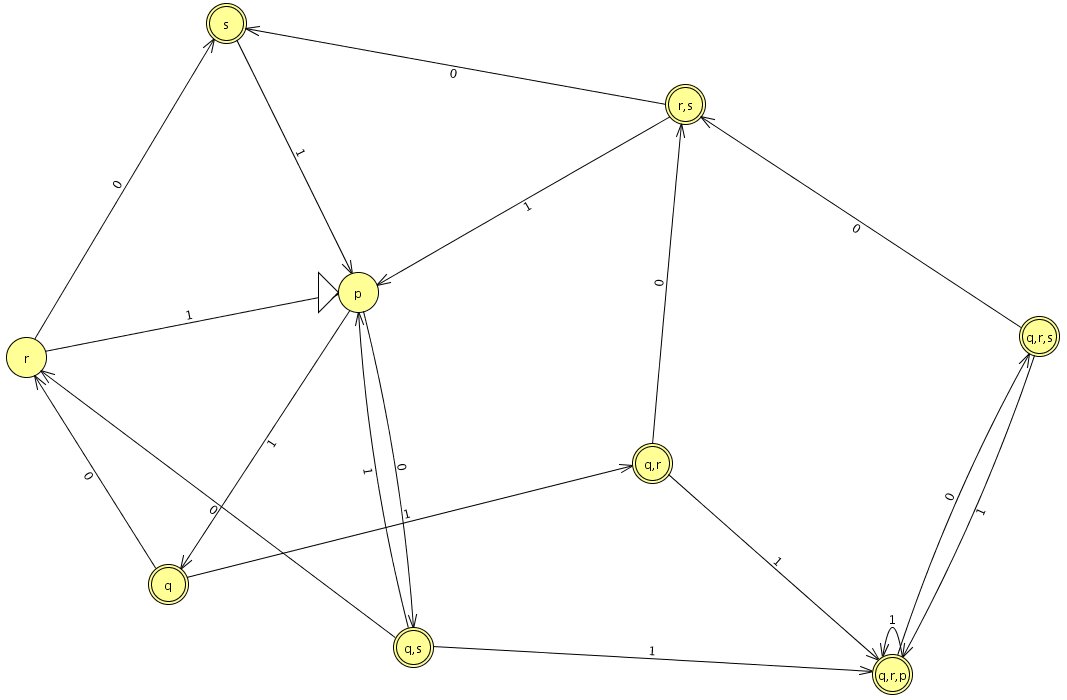
Tabelle und Transitionsdiagramm handschriftlich
Aufgabe 3a
`(0+1)^"*"000(0+1)^"*"`
"intuitiv": Zustände merken sich, wie viele Nullen bereits gelesen wurden
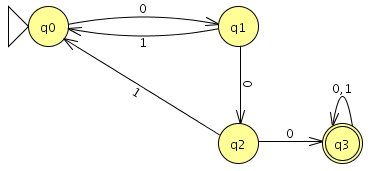
Aufgabe 3b
Anmerkung: Diese Aufgabe haben wir aufgrund ihres Umfangs nie kontrolliert, also habe ich auch keine Musterlösung zur Verfügung.
Für die, die es versuchen möchten: Prinzipiell geht es darum ein fünf Zeichen langes Fenster über den String zu legen und auf einsen zu checken. Zuerst muss man für genau fünf Zeichen den kompletten Baum aufspannen und gezielte Rücksprünge machen, damit die Länge genau fünf bleibt und der String mind. zwei Einsen enthält.
Aufgabe 3c
Potenzmengenkonstrukt
Regulärer Ausdruck ist: `(0+1)^"*"0(0+1)(0+1)`
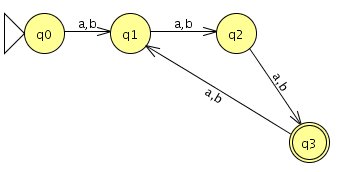
Daraus lässt sich folgender NEA ableiten:
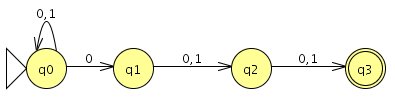
Die zugehörige Übergangstabelle:
| `delta` | `0` | `1` |
| `p` | `p,q` | `p` |
| `q` | `r` | `r` |
| `r` | `s` | `s` |
| `s` | `-` | `-` |
Nun muss die Potenzmenge gebildet werden.
| `delta` | `0` | `1` |
| `p` | `p,q` | `p` |
| `q` | `r` | `r` |
| `r` | `s` | `s` |
| `s` | `-` | `-` |
| `{p,q}` | `{p,q,r}` | `{p,r}` |
| `{p,q,r}` | `{p,q,r,s}` | `{p,r,s}` |
| `{p,r}` | `{p,q,s}` | `{p,s}` |
| `{p,q,r,s}` | `{p,q,r,s}` | `{p,r,s}` |
| `{p,r,s}` | `{p,q,s}` | `{p,s}` |
| `{p,q,s}` | `{p,q,r}` | `{p,r}` |
| `{p,s}` | `{p,q}` | `{p}` |
Nach Konvertierung mittels JFLAP (siehe Tools-Abschnitt) ergibt sich folgender DEA:
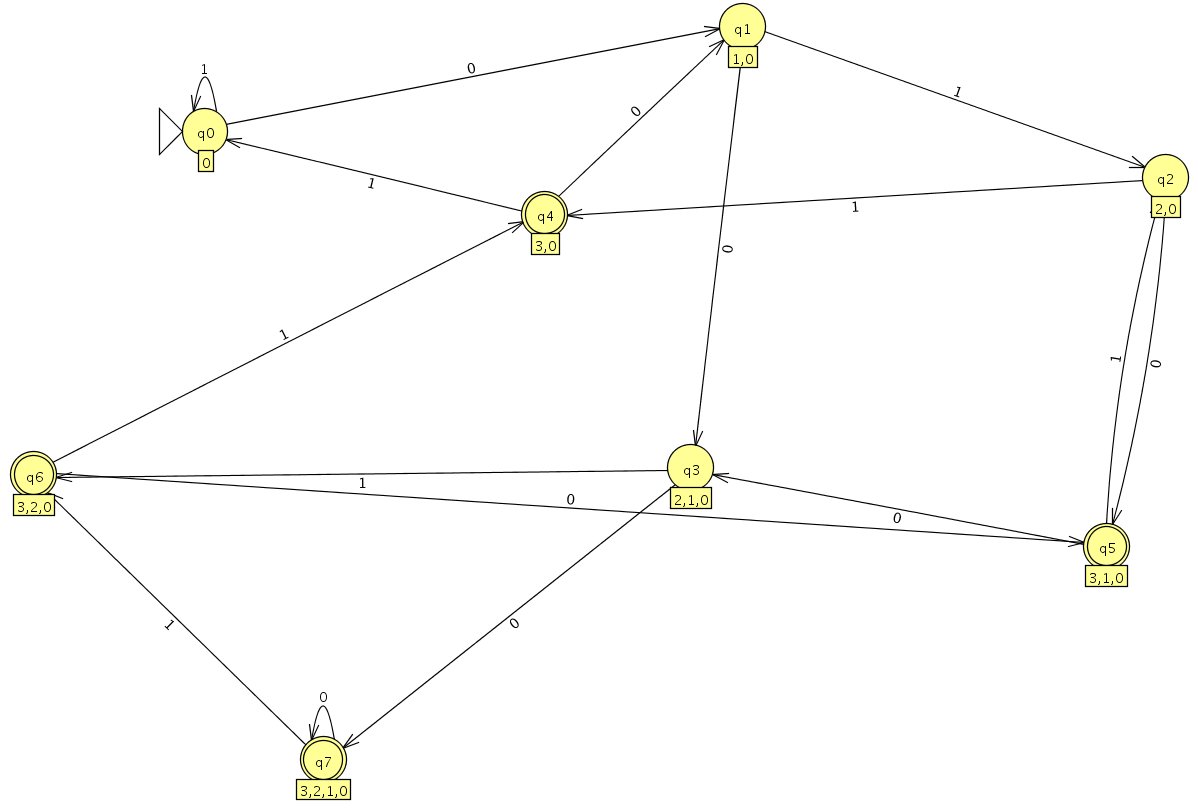
Aufgabe 4
Sind die Palindrome über `{a,b}` regulär?
Beweis durch Widerspruch mittels Pumping-Lemma
Annahme: L ist regulär (Anm. wird später widerlegt)
Mit dieser Annahme lautet das Pumping-Lemma wie folgt:
Es gibt ein `n in NN`, so daß für jedes Wort `x in L" mit "|x|>=n` eine Zerlegung `x=uvw` existiert mit `|uv|<=n` und `|v|>=1` und `uv^iw in L` für jedes `i in NN`. Ich habe da meine eigene unwissenschaftliche und evtl. falsche Interpretation.

Wie jetzt?
Ich habe hier ein paar Gedanken über diesbezüglich wichtig erscheinende Dinge niedergeschrieben.
Aufgabe 5a
`A = ({p,q,r},{a,b},delta_1,p,{r})`
`A_"regex" = ab(ab)^"*"=ab^+`

Aufgabe 5b
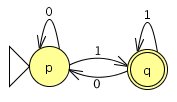
`A=({p,q},{0,1},delta_2, p, {q})`
`A_"regex" = 0^"*"1((0^+1^+)+1^"*"))`
Aufgabe 6
a)
Die Zeichenketten unterteilen sich in einen vorderen Teil, bestehend aus beliebig vielen Gruppen von geradzahlig vielen Einsen - jeweils getrennt durch eine beliebige Anzahl von Nullen - gefolgt von einem hinteren Teil, bestehend aus beliebig vielen Gruppen von geradzahlig vielen Nullen - jeweils getrennt durch eine beliebige Anzahl von Einsen.
An der "Nahtstelle" zwischen diesen zwei Teilen kann sich einen ungerade Anzahl Nullen oder Einsen ergeben. Sowohl der vordere als auch der hintere Teil können fehlen.
b)
Beliebige Zeichenketten über `{0,1}`, die höchstens zwei aufeinanderfolgende Nullen enthalten.
Aufgabe 7
a)
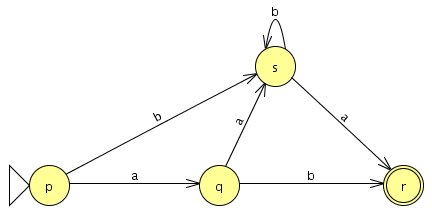
b)
im Moment zu groß... vielleicht später...
Aufgabe 8
a) `S -> 0S0 | 1S1 | 0 | 1 | epsilon |`
b) `S -> (S) | epsilon | SS`
alternativ geht auch `S -> () | (S) | ()S`
c)
`S -> {{:(epsilon |),(S011 | 0S11 | 01S1 | 011S |),(S101 | 1S01 | 10S1 | 101S |), (1S10 | 11S0 | 110S):}`
alternativ (nicht überprüft):
`{:(S -> A 0 A | A A 0 | 0 A A | epsilon),(A -> 1S | S1):}
d)
`{:(S -> a A a | b A b | a B b | b B a), (B -> epsilon | A | a B | b B), (A -> a | b | S):}
Aufgabe 9
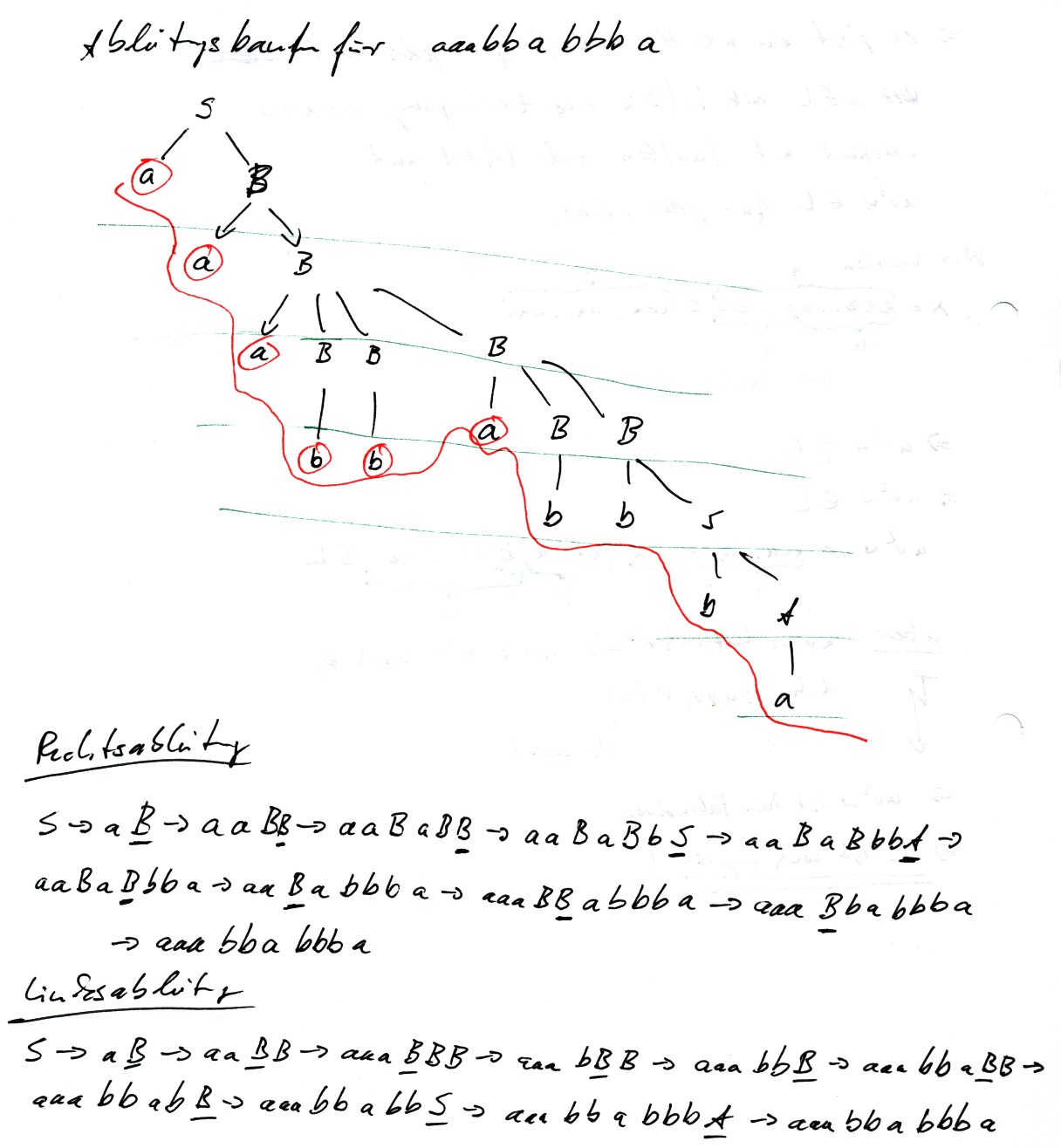
`{:(S -> a B | b A),(A->a | a S | b A A),(B->b | b S |a B B):}
Ableitungsbaum für aaabbabbba
Aufgabe 10
`S -> "<string 1>" | "<string 2>" | "<string 3>" | ... | "<string n>"`
Regulärer Ausdruck: `("<string 1>" + "<string 2>" + ... + "<string n>")^+`
Da ein regulärer Ausdruck existiert, gibt es auch einen endlichen Automaten.
Dieser entspricht den "parallel geschalteten" Automaten, die die einzelnen Strings erkennen.
Aufgabe 11
Da die Grammatik nur linkslineare Produktionen enthält ist sie vom Chomsky-Typ 3, also eine reguläre Sprache, was bedeutet, dass ein endlicher Automat möglich ist.
Ableitungsbaum
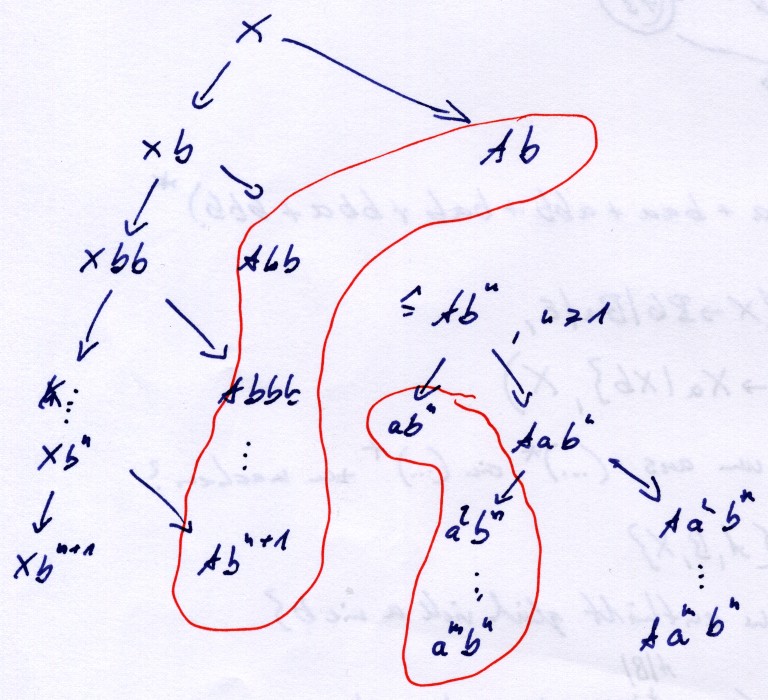
Daraus folgt: `L(G) = {a^m b^n| m,n > 0 }`. Das entspricht dem regulären Ausdruck `a a^"*" b b^"*" = a^+ b^+`
Aufgabe 12
Ja, es gibt eine solche Grammatik.
Regulärer Ausdruck
`(( a | b) ( a | b) ( a | b))^+`
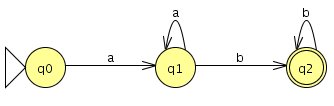
Endlicher Automat
Grammatik
Der reguläre Ausdruck lässt sich auch wie folgt schreiben: `(a a a + a a b + a b a + b a a + a b b + b a b + b b a + b b b)^+`
Daraus bilden wir die Grammatik `G`:
`G = ({X,A,B}, {a,b}, {X -> Bb|Ba|epsilon, B -> Aa|Ab, A -> Xa|Xb}, X)`
Aufgabe 13
1)
`X-> a b | b a | X X | a X b | b X a`
2)
`X -> a B | b A, B -> b | b X | a B B, A -> a | a X | b A A`
Aufgabe 14
a)
Ja, die Menge ist regulär, da Iterationen, Konkatenationen und Vereinigungen regulärer Mengen wieder reguläre Mengen erzeugen.
b)
`b a^"*" b + a a^"*" b a = b a^"*" b + a^+ b a`
Aufgabe 15
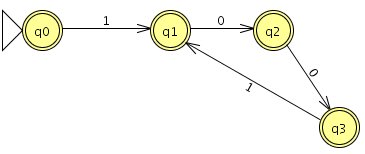
Regulärer Ausdruck: `epsilon + 1 + 10 + (100)^+ + (100)^+1 + (100)^+10`
Aufgabe 16
`{:( ack(0,y),=,y+1 ),( ack(x+1,0),=,ack(x,1) ),( ack(x+1,y+1),=, ack(x, ack(x+1,y)) ):}`
`{:( f_0(y), =, ack(0,y), =, y+1, , ),( f_1(y), =, ack(1,y), =, ack(0,1), =, 2" für " y=0 ),( f_1(y), =, ack(1,y), =, ack(0,ack(1,y-1)), =, f_0(ack(1,y-1)) ),( , =, ack(1,y-1)+1, =, ack(0,ack(1,y-2)), =, f_0(ack(1,y-2))+1 ),( , =, ack(1,y-2)+2, =, ..., =, f_0(ack(1,y-y))+y ),( , =, ack(1,0)+y, =, ack(0,1)+y, =, 2+y" für "y>=1 ):}`
`=> f_1(y)=2+y`
Mitschrift für `f_2` und `f_3`
Aufgabe 17
a) `(a b)^+`, also mindestens ein mal `a b`
b) Es handelt sich um eine Typ-2-Grammatik, da sie Links- und Rechtsableitungen enthält.
c) ja, denn es gibt einen regulären Ausdruck.
`G_(Typ-3)=(N,T,P,X)" mit "T={a,b},N={X}" und" P={X->ab|abX}`
Aufgabe 18
siehe Aufgabe 11...
Aufgabe 19
a)
Zeichenketten bestehend aus identisch vielen `{a,b,c}`, wobei zuerst sämtliche a's stehen, gefolgt von einer Zeichenreiche aus `{b,c}`, wobei jedes Präfix dieser Zeichenreihe mindestens so viele b's enthält wie c's. (Mitschrift)
b)
Die Sprache ist vom Typ-0. (Wegen der Produktion `C C -> B C`)
c)
nein, Beweis durch Pumping-Lemma
Quellen
- Vorlesung "Grundlagen der Informatik 2" an der Fachhochschule Rosenheim
Tools
Gedanken des Autors
4
Auf Deutsch: Wir können jedes Wort aus `L`, was mindestens `n` Zeichen lang ist, in drei Teile (u,v und w) zerlegen. Dabei müssen jetzt die ersten beiden Teile zusammen weniger lang als n sein und der zweite Teil muss wenigstens ein Zeichen enthalten.
Is ja auch logisch. Ich nehm' was, was mindestens sooo lang is, zerleg das in zwei Teile und da muss der erste Teil weniger als sooo lang sein, wenn der zweite Teil auch ne Länge hat.
Das tolle am Pumping-Lemma is jetz, dass der erste Teil eigentlich aus zwei unterteilen besteht, nämlich u und v. Und ausserdem sagt das Pumping-Lemma, dass der zweite der unterteile immer wieder kommen kann und die oben gemachte Aussage immer noch gilt. (nämlich dass der erste große teil kleiner als die gesamtlänge is und der zweite teil wenigstens da sein muss.)
Wahrscheinlich ist das verwirrender als die eigentliche Defitionion, aber ich musste es einfach aufschreiben. ;)
4.1 Worauf es bei dem Beweis ankommt
Wir haben angenommen die Sprache sei regulär. Dann haben das Pumping-Lemma so interpretiert, dass wir ziemlich einfach widerlegen konnten, dass die Sprache regulär sei um schlussendlich zu folgern, dass sie nicht regulär ist. Beweis durch Widerspruch.
Salopp gesagt: Wir haben das Pumping-Lemma benutzt um die linke Seite wachsen zu lassen während wir die rechte beibehalten haben.
Was folgt daraus? Die Sprachdefinition ist nicht mehr erfüllt. <- Das ist an sich der Widerspruch.
Unser Beispiel kann nicht mehr a's vor dem b haben als danach, wenn es ein Palindrom sein will. Wir haben also gezeigt, dass wir mit Hilfe des Pumping-Lemmas ein Wort aus L so umwandeln können, dass es nicht mehr zur ursprünglichen Sprache gehört. Daraus haben wir geschlussfolgert, dass es sich bei L um keine reguläre Sprache handeln kann.