Ackermann-Funktion

Eine Form, mit der sich einfacher rechnen lässt:

`a(0,y) = y + 1`
`a(x,0) = a(x-1,1)`
`a(x,y) = a(x-1,a(x,y-1))`

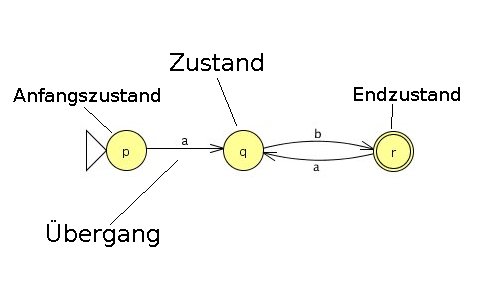
Automatendefinition

`A = (Q, Sigma, delta, I, F)`

`Q`	Menge der Zustände
`Sigma`	Eingabealphabet
`delta`	Zustandsübergänge
`I`	Anfangszustände
`F`	Endzustände

A = (Menge der Zustände, Eingabealphabet, Übergänge, Anfangszustände, Endzustände)

Chomsky Hierarchie

Stufe	Sprachen	Automaten	Regeln	Abgl.
Typ-3	regulär	(deterministischer) endlicher Automat	`A -> aB` (rechtsregulär) oder `A->Ab` (linksregulär) `A->a` `A,B in N`, `a in Sigma`	CKSV
Typ-2	kontextfrei	nichtdeterministischer Kellerautomat	`A -> gamma` `A in NN`, `gamma in V^"*"`	KV
Typ-1	kontextsensitiv	linear platzbeschränkte nichtdeterministische Turing-Maschine	`alpha A beta -> alpha gamma beta` `A in N`, `alpha, beta, gamma in V^"*"`, `gamma != epsilon`	CKSV
Typ-0	rekursiv aufzählbar (alle)	Turing-Maschine	`alpha -> beta` `alpha, beta in V^"*"`, `alpha != epsilon`	KSV

Mengensymbole

• `Sigma`: Menge der Terminale
• `N`: Menge der Nichtterminale
• `V = Sigma uu N`: Menge der Variablen

Abgeschlossenheit

• C = Komplementbildung
• K = Konkatenation
• S = Schnittmenge
• V = Vereinigungsmenge
• * = Kleenescher Abschluss

Grammatik

`G = (V, Sigma, P, S)`

`V`	Menge der Variablen (endlich)
`Sigma`	endliche Menge, sog. terminales Alphabet (die Operatoren), wobei `V sub Sigma = 0`
`P`	Produktionen/Regeln
`S`	Startvariable

G=(Menge der Variablen, terminales Alphabet, Produktionen/Regeln, Startvariable)

Beim Erstellen darauf achten, ob `epsilon`, also die leere Menge, mit zur Menge gehört.

Potenzmengenkonstrukt

Es werden für alle "Doppel-Belegungen" neue Zustände eingeführt. Im Beispiel ist das `{p,q}`.

`delta`	`0`	`1`
`p`	`p,q`	`p`
`q`	`p`	`p`
`{p,q}`	`{p,q}`	`p`

Checklist

1. alle Potenzmengen in Tabelle
2. Automat von Start aufbauen (siehe Automatendefinition)
3. Endzustände einzeichnen (siehe Automatendefinition)
4. Probe: Pfeile zählen (Anzahl der Zustände x 2 - "Leerstellen")

Sprache

Sprachen werden aus Grammatiken abgeleitet. Sei `G = (V, Sigma, P, S)` und `u,v in (V uu Sigma)*`:

1. `v` heisst aus `u` direkt ableitbar, wenn `alpha, beta, gamma, delta in (V uu Σ)^"*"` existieren, so dass gilt:
   

`alpha → beta in P` und `u = gamma alpha delta` und `v = gamma beta delta`.
Wir schreiben `U => V`

1. `u` heisst Satzform von `G` wenn gilt `S -> U`
2. `u` heisst Satz von `G`, wenn `u` eine Satzform von `G` ist und gilt: `u ∈ Σ^"*"`
3. Die Menge aller Sätze von `G` heisst die von `G` erzeugte Sprache und wird mit `L(G) = {u in Sigma^"*" |S -> u}` bezeichnet.

`L(G)= { u in Sigma^"*" | S -> u }`

Transitionsdiagramm

Die grafische Darstellung eines Automaten.